Geometric frustration
Geometric frustration of interactions implies that there are multiple possible quantum ground states with very close energies. It takes a very small push, such as the application of a magnetic field or perhaps some small anisotropy terms in the Hamiltonian to pefer one such state over another. One dimensional systems where quantum fluctuations are strongly enhanced to begin with are particularly prone to this kind of behavior. But not necessarily: frustration may have profound consequences in higher dimensions as well.
Linear-chain ferro-antiferromagnets
![Enlarged view: (a) Magnetic torque curves (left panel) and their derivative (right panel) for H ‖ b in Cs<sub>2</sub>Cu<sub>2</sub>Mo<sub>3</sub>O<sub>12</sub>. (b) Magnetic phase diagram in a magnetic field applied along b axis [1].](/highlights/spin-nematics-and-presaturation-phases/_jcr_content/par/textimage_566343959/image.imageformat.text50percent.1432461281.png)
One deceptively simple model is the frustrated ferro-antiferromagnetic spin chain. In our lab we have grown the only known single crystal samples of two very interesting materials of this type, namely Rb2Cu2Mo3O12 and Cs2Cu2Mo3O12. This enabled us to perform comprehensive magnetic and thermodynamics measurements that were previously unthinkable for powder samples. For these two systems we found completely different phase diagrams, more complex than anyone expected.
The Rb compound [1] has a gapped non-magnetic ground state, but shows a "bubble" of field-induced magnetic long range order. Interestingly, the first field-induced quantum phase transition is of a 3-dimensional character, while the second is dominated by one-dimensional fluctuations. For different field directions the phase diagrams are rather distinct, indicating the huge role of magnetic anisotropy.
The Cs material [2] is already ordered in zero field. In applied fields there is an entire cascade of novel phases. Regardless of field geometry there is a narrow presaturation phase that is likely a spin nematic order or other multimagnon condensate.
[1] D. Flavián, S. Hayashida, L. Huberich, D. Blosser, K. Yu. Povarov, Z. Yan, S. Gvasaliya, A. Zheludev, external page Phys. Rev. B 101, 224408 (2020).
[2] S. Hayashida, D. Blosser, K. Yu. Povarov, Z. Yan, S. Gvasaliya, A. N. Ponomaryov, S. A. Zvyagin, and A. Zheludev, external page Phys. Rev. B 100, 134427 (2019).
Subtle effects of anisotropy
![Enlarged view: Measured magnetic phase diagram of linarite supporting helimagnetic, conical, colinear and spin-density-wave quantum phases [3].](/highlights/spin-nematics-and-presaturation-phases/_jcr_content/par/textimage_1136737767/image.imageformat.text50percent.827390325.png)
Another very interesting quasi-one-dimensional ferro-antiferromagnet is PbCuSO4(OH)2. In applied magnetic fields it shows a number of very unusual quantum phases, including a spin density wave state. Magnetic anisotropy, particularly so-called Dzyaloshinkii-Moriya interactions play a central role in this behavior. To figure this out, we used magnetic torque measurements to map out the three-dimensional magnetic phase diagram [3]. We didn't even need to grow our own single crystals: this compound is naturally available as the mineral linarite.
[3] Y. Feng, K. Yu. Povarov, A. Zheludev, external page Phys. Rev B. 98, 054419 (2018).
Anisotropy and the triangular lattice
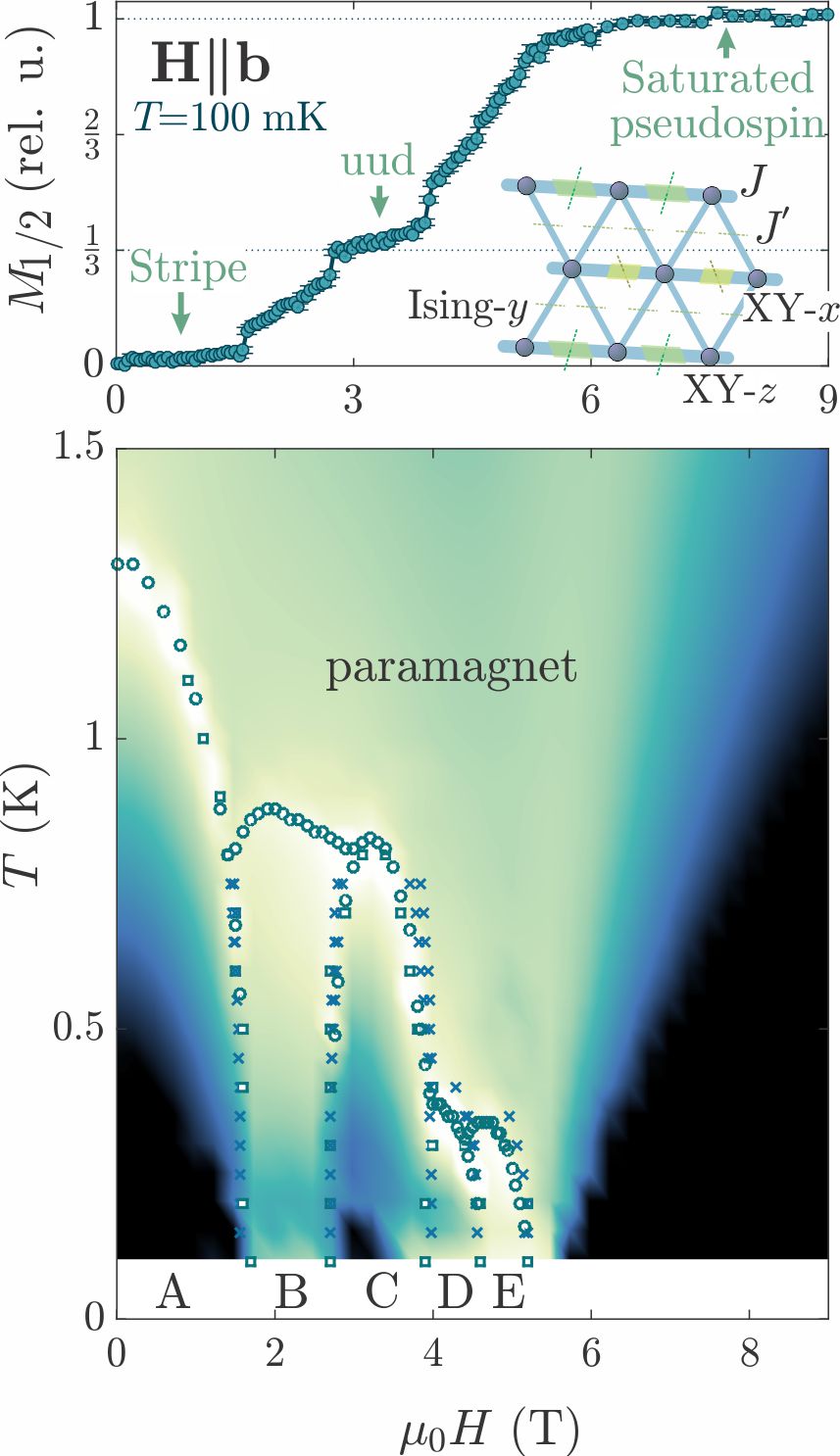
Frustration refers to a competition of several interactions. However, frustration can also be caused by magnetic anisotropy. This is common in spin ices or in Kitaev magnets. We have found a new material where the "anisotropy vs exchange" interplay results in a very complicated Hamiltonian. The material is Cs2CoBr4 with S=3/2 cobalt magnetic ions forming parallel chains coupled by zig-zag interaction. This Hamiltonian is frustrated on its own, but it’s the extreme easy-plane anisotropy to run the game: only S=1/2 pseudospin degrees of freedom survive, and the quantization axis is alternating between the chains. The effective Hamiltonian is characterized by direction-dependent bonds, and the material itself shows an astonishingly complex phase diagram with up to 5 phases [1]. Some are magnetization plateaux, including the famous up-up-down phase, typical of lattices with triangular exchange patterns. One of the magnetizable phases is a spin-density wave (SDW), the first ever observed in a triangular system [2]. We measured the dynamics in this curious 2D SDW phase and found notable differences from SDWs occurring in 1D chains.
[1] K. Yu. Povarov, L. Facheris, S. Velja, D. Blosser, Z. Yan, S. Gvasaliya, A. Zheludev, external page arXiv:2004.09893 (2020).
[2] L. Facheris, K. Yu. Povarov, S. D. Nabi, D. G. Mazzone, J. Lass, B. Roessli, E. Ressouche, Z. Yan, S. Gvasaliya, A. Zheludev, external page Phys. Rev. Lett. 129, 087201; external page arXiv:2204.10682 (2022).