Quantum multiferroics
Multiferroics are materials with coupled magnetic and ferroelectric order. The underlying microscopic mechanism is rooted in relativistic spin-orbit intearactions. For obvious reasons, multiferroics are of great industrial significance. We, however, are more interested in fundamental aspects. Which exotic phases of quantum magnetic materials have electrical polarization? What can we learn about the magnetic system and magnetic quantum phase transitions by studying dielectric properties? Is it possible that dielectric degrees of freedom play an active role in quantum phase transitions and collective excitations?
Improper ferroelectricity at a magnetic quantum phase transition
![Enlarged view: Dielectric anomalies measured isothermally at different magnetic field in quantum multiferroic Sul-Cu<sub>2</sub>Cl<sub>4 </sub>[2].](/highlights/quantum-multiferroics/_jcr_content/par/textimage_1659340314/image.imageformat.text50percent.230810604.png)
Sul-Cu2Cl4 is a peculiar quasi-one-dimensional "spin tube" system. The ground state is non magnetic, but an external magnetic field induces long-range helimagnetic order, following a Bose-Einstein condensation (BEC) of magnons quantum phase transition. Due to peculiarities of the crystal structure the incommensurate helimagnetic phase supports a ferroelectric polarization. Despite initial reports by another group (who too used our samples) [1], this is an improper ferroelectric, meaning that electrical polarization is not the primary order parameter [2]. It is not critical at the transition, but nontheless shows a very strong anomaly at the transition point, which can be very precisely measured. In this way, through dielectric experiments we are able to obtain a very accurate measurement of the BEC crossover exponent. In addition we study the highly non-linear dielectric response within the ordered phase.
[1] F. Schrettle, S. Krohns, P. Lunkenheimer, A. Loidl, E. Wulf, T. Yankova and A. Zheludev, external page Phys. Rev. B 87, 121105(R) (2013).
[2] K. Yu. Povarov, A. Reichert, E. Wulf and A. Zheludev, external page Phys. Rev. B 92, 140410(R) (2015).
Multiferroic phases of linarite
![Enlarged view: Pyroelectric current measurements of electrical polarization in linarite [3].](/highlights/quantum-multiferroics/_jcr_content/par/textimage_516494836/image.imageformat.text50percent.890272704.png)
Magnetization is an axial vector, but electrical polarization a polar one. Out of symmetry considerations, the two can only couple if there is another axial vector in the system. Very often such is the vector of pseudochirality in a helimagnetic structure. The frustrated quasi-one-dimensional material PbCuSO4(OH)2 (linarite) has a very complicated phase diagram in applied magnetic fields. Some of these phases are ferroelectric, while others fail to satisfy the above-mentioned symmetry requirements. By measuring the direction of electrical polarization in this compound we are able to deduce the spin arrangements in the multiferroic incommensurate phases [3].
[3] K. Yu. Povarov, Y. Feng and A. Zheludev, external page Phys. Rev. B94, 214409 (2016).
True multiferroic quantum criticality
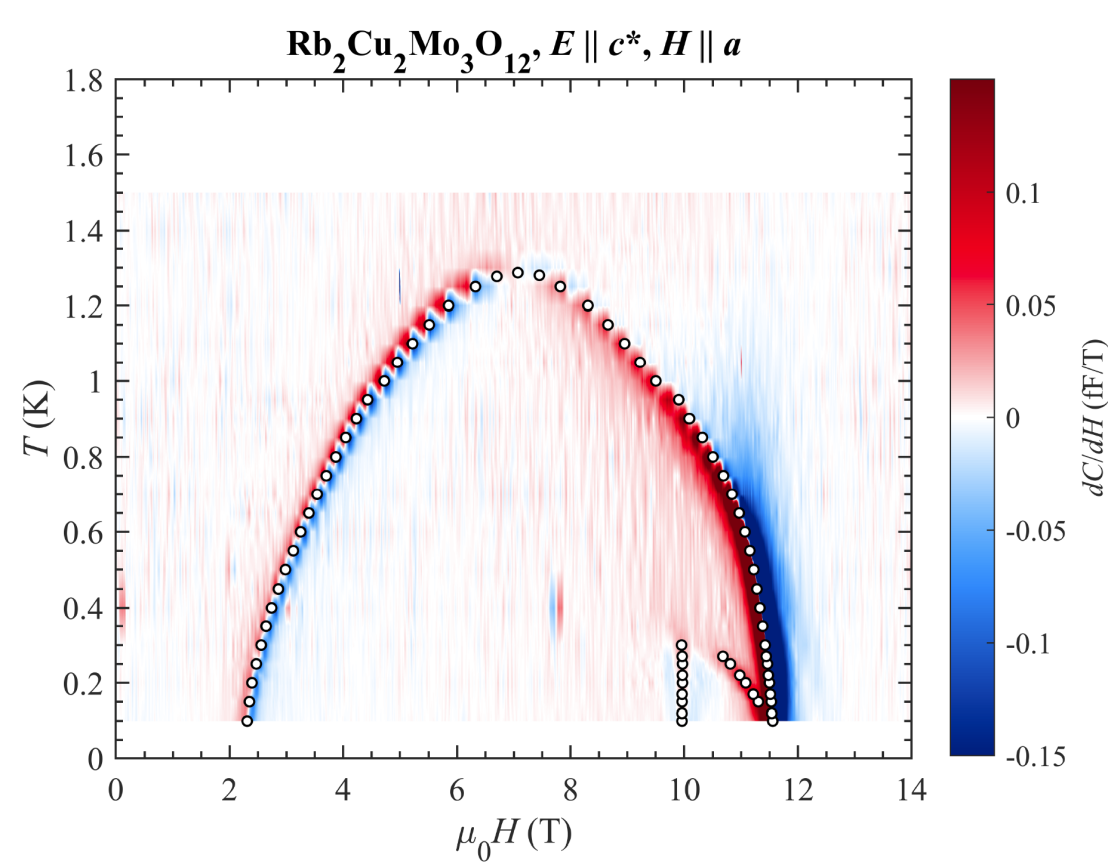
Shhh! A brand new unpublished result. The linear-chain ferro-antiferromagnet Rb2Cu2Mo3O12 has been celebrated in literatuire as an example of a chiral spin liquid. In zero magnetic field it doesn't order at all, and has a very interesting magnetic phase diagram in appled fields [4]. All magnetically ordered states are confined to below 1.5 K. And yet, in applied fields the material becomes ferroelectric at 8 K. The conclusion was that chirality appears before conventional magnetic order.
Not so fast... All previous dielectric measurements were performed on powder samples. In our group we were the first to synthesize single crystals of this material. It turns out that the 1.8 K anomaly is an artefact present only in scintered powders and absent in proper polycrystals and single crystals. The material is, indeed, ferroelectric, but only in the magnetically ordered state. Even better, this system is a proper ferroelectric. This means that electrical polarization is the primary order parameter of the field-induced quantum phase transition. All critical exponents can be directly measured in the dielectric channel!
[4] S. Hayashida, D. Blosser, K. Yu. Povarov, Z. Yan, S. Gvasaliya, A. N. Ponomaryov, S. A. Zvyagin, and A. Zheludev, external page Phys. Rev. B 100, 134427 (2019).