Defective quantum magnets
Take a "classical" magnetic system, say an antiferromagnet, and create a defect by removing one spin. The remaining spins will remain aligned in a antiferromagnetic Neel structure as if nothing happened. Not so for a quantum magnet, where in the ground state all spins are subject to collective zero-point fluctuations. Removing one spin will drastically affect the fluctuations of the remaining neighbors. Most unusual phenomena may arise as a result.
For real materials, replacing a few magnetic ions with non-magnetic ones can usually be incorporated into the sample growth process. The problem can thus be addressed experimentally.
Spin islands in a depleted spin ladder
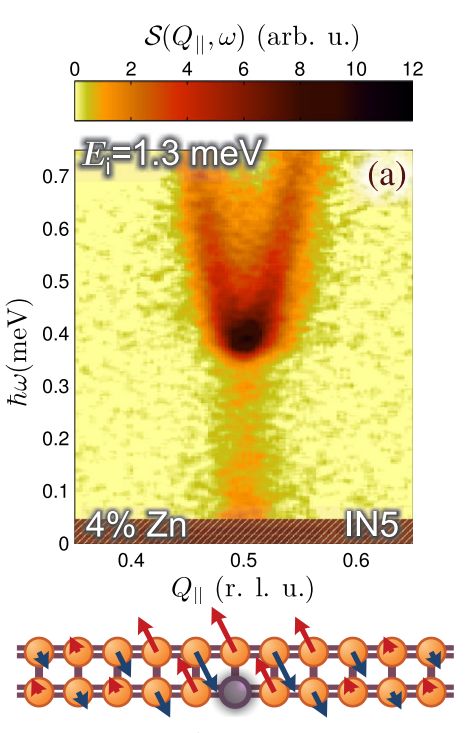
Take a quantum spin system with a non-magnetic ground state protected by an energy gap, say a spin ladder. Now remove a few spins. Paradoxically, what remains will become magnetic and gapless!
The emergent magnetism is due to new degrees of freedom that are "liberated" when quantum fluctuations in the vicinity of the defect are suppressed. They can be visualized as localized islands of staggered polarization. They have a non-zero total magnetic moment and thus react to the external magnetic field. They may partially overlap and thus interact with one another, thereby acquiring a dynamics of their own.
We study this phenomenon in the strong leg spin ladder DIMPY [1]. It can be easily depleted by replacing the S=1/2 copper with S=0 zinc ions during crystal growth. The ladder topology ensures that magnetic continuity remains intact. The spin islands are of several lattice units in size. Interactions between them fall off with distance and are sign-alternating. One effectively gets a chain of island-spins coupled with random interactions. We studied this model numerically and found spectacular agreement with experiments on Zn-substituted DIMPY. The dynamics of the effective island-chains is readily observable in a neutron scattering experiment as a weak in-gap excitation continuum. This scattering contains information on the shape of the spin island in real space. Further insight is obtained in electron spin resonance (ESR) experiments [2].
[2] D. Schmidiger, K. Yu. Povarov, S. Galeski, N. Reynolds, R. Bewley, T. Guidi, J. Ollivier, A. Zheludev, external page Phys. Rev. Lett. 116, 257203 (2016).external page
[3] Yu. V. Krasnikova, V. N. Glazkov, A. Ponomaryov, S. Zvyagin, K. Yu. Povarov, S. Galeski and A. Zheludev, external page Phys. Rev. B 100, 144446 (2019).
Pseudogap in depleated spin chains
![Enlarged view: Top: The local correlation function in defective spin chain materials does not scale as in a defect-free spin chain. Bottom: The scaling is restored if the corresponding envelope functions are factored out. No adjustable parameters [2]!](/highlights/defects-in-quantum-magnets/_jcr_content/par/textimage_2000779871/image.imageformat.text50percent.1934846266.png)
Now take a gapless magnetic material and remove a few spins. What will happen? A trick question! In some cases the system will open a gap.
The oxides Sr2CuO3 and SrCuO2 are among the oldest known Heisenberg spin chain compounds with very large energy scales. A lot of excitement was caused by the observation that only ultra-pure materials show any long range magnetic order at low temperatures and that even less than 1% of impurities opens a sizeable gap in the spin excitation spectrum. Wild theories abound. Our neutron experiments have revealed the true origin of this behavior [3]. Unlike in a spin ladder, any defect entirely breaks the spin chain continuity, breaking it up into fragments. Boundary conditions ensure that the momentum (and therefore energy) of spinons propagating in such fragments is discretized. The spectrum becomes gapped. A random distribution of fragment length leads to a random distribution of gaps and an effective pseudogap in a macroscopic sample. The problem can actually be solved analytically. The resulting excitation spectrum is as that of a defect-free chain times a defect-concentration dependent envelope function. Measuring the spectrum in different materials, at different temperatures and with different defect concentration, and factoring out the envelope function results in data that collapses onto a single universal curve [4].
Further measurements using muon spin rotation explored the effect of defects on long-range ordering, confirming the theoretically predicted "LT-scaling" in this problem [5].
[3] G. Simutis, S. Gvasaliya, M. Mansson, A. L. Chernyshev, A. Mohan, S. Singh, C. Hess, A. T. Savici, A. I. Kolesnikov, A. Piovano, T. Perring, I. Zaliznyak, B. Buchner, A. Zheludev, external page Phys. Rev. Lett. 111, 067204 (2013).
[4] G. Simutis, S. Gvasaliya, N. S. Beesetty, T. Yoshida, J. Robert, S. Petit, A. I. Kolesnikov, M. B. Stone, F. Bourdarot, H. C. Walker, D.T. Adroja, O. Sobolev, C. Hess, T. Masuda, A. Revcolevschi, B. Büchner, A. Zheludev, external page Phys. Rev. B 95, 054409 (2017).
[5] G. Simutis, M. Thede, R.Saint-Martin, A. Mohan, C. Baines, Z. Guguchia, R. Khasanov, C. Hess, A. Revcolevschi, B. Buchner, A. Zheludev, external page Phys. Rev. B 93, 214430 (2016).